Old blog - New website!

I am no longer adding posts to this old blog.  But do please check out my new website, sebfalk.com!

There you'll find all my latest blog posts, as well as details about my work, and my new book, The Light Ages!



Thanks to all the people who've read this blog over the years.  I look forward to reading your comments on the new blog.

John Gower and the Gruffalo

Back in June I was thrilled to get another chance to broadcast an Essay on BBC Radio 3.  This one was about John Gower, "the forgotten medieval poet".  So I dusted off my Middle English, paid a quick trip to Southwark Cathedral, and did my best to convey the amazing range of this 14th-century Kentish curmudgeon.

"Here lies John Gower, poeta celeberrimus"

You can listen now at https://www.bbc.co.uk/programmes/b0b7hvgy.  It was recorded with a live audience at the fantastic York Festival of Ideas.  I did get rather carried away with this passage from the Confessio Amantis:

Medea with hire art hath wroght Of cloth of gold a mantel riche, Which semeth worth a kinges riche, And that was unto Creusa sent In name of gifte and of present, For sosterhode hem was betuene; And whan that yonge freisshe queene That mantel lappeth hire aboute, Anon therof the fyr sprong oute And brente hir bothe fleissh and bon. Tho cam Medea to Jason With bothe his sones on hire hond, And seide, 'O thou of every lond The moste untrewe creature, Lo, this schal be thi forfeture.' With that sche bothe his sones slouh Before his yhe, and he outdrouh His swerd and wold have slayn hir tho, Bot farewel, sche was ago

Stirring stuff! And a very similar metre to that used by Julia Donaldson, as I explain in my programme.

Girton College Mappa Mundi

Girton College, the Cambridge University college where I am lucky to work, owns a full-scale facsimile of the Hereford Cathedral Mappa Mundi.  It was given by Girton alumna Dr Margaret Mountford (yes, the one from The Apprentice) and hangs in a corridor near the college hall.

I've walked past it so many times that I thought I should sit down and take a closer look.  Here are a few things I found (presented in the form of some tweets I posted).

In a way it’s Even Better Than The Real Thing, as it was digitally enhanced to approximate the colours of the c.1300 original.

It was made from a whole calfskin, 5’2” (159cm) high, 4’4” (132cm) wide. At top sits Christ in judgement: saved on his right, doomed on left.

This is God’s world, & further reminder of our fate is MORS (death) spelled out in gold letters around the edge.  Here’s the M.

The M is in the northeast: you can see the O’s where “septemtriO” meets “Oriens”.  Underneath you can see Wlturnus, one of the 12 winds.

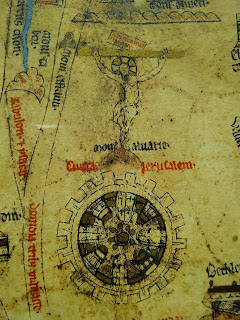
The map is both deeply symbolic and the product of careful scholarship. At the centre is Jerusalem, with the crucified Christ above.

The north coast of the Mediterranean Sea (on the left: E is up) also traces the curve of Christ’s body, with the Cyclades islands marking his head.

Here Noah’s ark “came to rest in the mountains of Armenia”.









There’s plenty of geographical detail. Here it says the length of AFFRICA from Ethiopian Sea to Alexandria is 1725 miles.

But note he’s written “longitudo” twice; he realised his mistake, put dots under the second one & added “Lat” to correct it to latitude.



But one big mistake that wasn’t corrected is that Africa was accidentally labelled “EUROPA”, and vice versa!

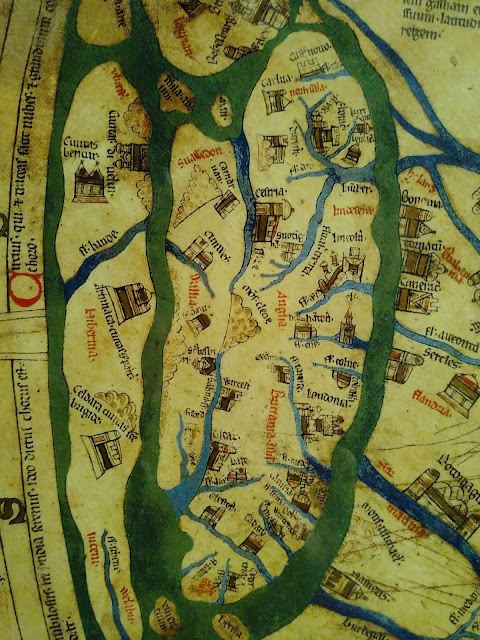
Britain & Ireland show huge local knowledge.  Lincoln is particularly detailed, not surprising since the map was probably designed there.

The river Tweed is shown separating England & Scotland, with Edinburgh castle on its Rock (& Roxburgh, Berwick & St Andrews)

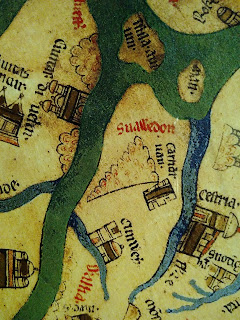
Here is Snowdon, just across the sea from Dublin (civitas divelin).

Here are Armagh, city of St Patrick, & Kildare, city of St Brigid.  Across the sea there’s Shrewsbury, the Severn, Worcester & Hereford.

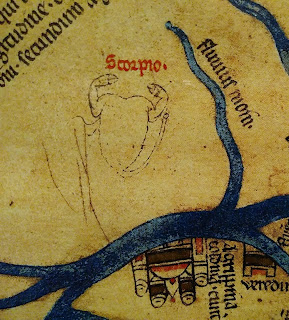
 There’s less astronomy than I expected [EDIT: not that one would naturally expect astronomy on the largely symbolic mappae mundi, but this one is cosmologically compendious and its designer had clearly read his Martianus Capella and Pliny.  It is overall rather more scientifically informed than previous historians have given it credit for.].  Just two possible (unlikely) references to the zodiac: Taurus (“Buglossa”) and Scorpio:

There’s a bear near Scandinavia (note also the Norwegian on skis, & the Griste people who make saddles from the skins of their enemies)

















At the bottom the map’s designer (?), Richard of Holdingham, is identified with biblical and classical allusions.


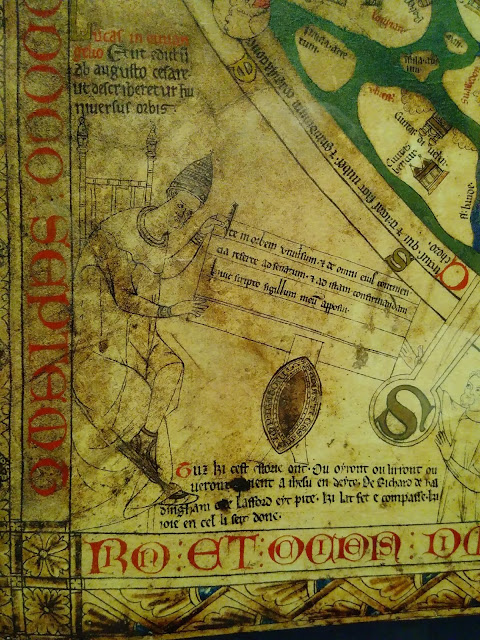
Above is a passage from Luke’s gospel: “there went out a decree from Caesar Augustus that the world should be described”.

Augustus (with papal tiara) hands his instructions to 3 classical geographers.  In the middle is the S of MORS.








It’s been suggested that the map was vandalised by someone who didn’t like Paris (note the I of “Affrica” at the top right).

Let’s not forget the famous mythical people, like the Monoculi who shade themselves from the Indian sun with their one huge foot.

There’s so much rich & precise detail, drawing on at least a dozen sources.  Why not visit Hereford Cathedral (or study at Girton College) & see it for yourself?

Heat, Comets, and Collaboration

This post is cross-posted from the Ordered Universe project blog (with different pictures).

The 18th Ordered Universe symposium – and the fourth held under the sponsorship of the Arts and Humanities Research Council – took place in Oxford, at Pembroke College,  on 17-19 May. We were wonderfully hosted by the College, with lunches and dinners held in its magnificent Victorian Gothic hall; the symposium organisation was smoothly handled by Pembroke fellows Hannah Smithson and Clive Siviour, with indispensable help from DPhil students Joshua Harvey and Tim Farrant.

The symposium focused on an interdisciplinary reading of two treatises, De impressionibus elementorum (On the Impressions of the Elements) and De cometis (On Comets). These can be placed in the middle of Robert Grosseteste’s scientific development, showing traces of his early alchemical interests but also hints of his developing argumentative technique and increasing interest in the nature of light.

We worked quickly through De impressionibus elementorum on the first day (starting from an impressive draft translation made by Sigbjørn Sønnesyn). ‘On the impressions of the elements’ is perhaps a misleading title (and is only found in two of the seven manuscript copies), as the text really concerns what we might today call the states (or even cycle) of water. Grosseteste’s discussion of icy waters, and of fog, dew, rain and snow, centres on the kinds of heat that cause evaporation. So the group spent some time discussing the nature of bubbles, and how they might be ‘dense’ or ‘subtle’, as Grosseteste explains. We were also very interested in his arguments about the layers and overall height of (what we would now call) the atmosphere.

On the second and third days we discussed Grosseteste’s longer De cometis. In this treatise, Grosseteste spends some time establishing a range of incorrect opinions about comets and their tails – opinions, he says, held by people who have observed comets but not thought carefully about them. He explains how comets must be fire that has risen up from the earth and is influenced by a star or planet. They strike fear into the hearts of people whose fortunes will be affected by them! The variety of words Grosseteste uses for the tail of these hairy stars gave us much to discuss, between the relative merits of ‘tress’, ‘trail’, ‘braid’ and so on…

Aside from our collaborative translations, we heard presentations from Francesca Galli (Università della Svizzera Italiana), Brian Tanner and Cecilia Panti, who shared their research into these or related materials.

This was my first Ordered Universe symposium, and I loved every minute of it. Two rules were explained at the outset: (1) there are no stupid questions; and (2) participants were explicitly encouraged to make suggestions and take part in discussions away from their area of academic expertise. In practice, as we progressed steadily through the translation, a half-dozen of the twenty scholars round the table did most of the talking about the finer meanings of Latin vocabulary and how best to render words in English. But whenever we got stuck for a minute on what Grosseteste meant when he stated a fact about nature or gave an explanation of causes, that’s when the discussion really opened up. A scientist might draw an analogy with phenomena observed using modern methods, or give a vivid interpretation of Grosseteste’s meaning using a laser pointer and a glass of diluted milk (see photo). These excursus into subjects ranging from water’s unique freezing properties to gravitational lensing were entertaining and enlightening; I did wonder whether the scientists were getting as much benefit from their participation as they were contributing – but occasional bursts of enthusiastic speculation about wacky experiments that might be performed to test Grosseteste’s ideas suggested that they were getting morsels of inspiration for their work.

Reading such fascinating texts with a lovely group of sharp and generous scholars expert in a wide range of disciplines, was a tremendous privilege and a great learning experience. I’d like to thank all the established participants who welcomed me so kindly, and – in addition to those named above – especially Giles Gasper for chairing our discussions so patiently.

Not Grosseteste but Tove Jansson

How short is the shortest day?

Happy Yule!  As you probably know, Yule (Jól) was the pagan Nordic celebration of the bleak midwinter.  And it's the winter solstice today - the shortest day of the year.

Ring of Brodgar (from @VisitScotland via @HistoryNeedsYou)

What does that mean?  The word solstice means "stopped Sun" in Latin - so it's not really a whole day, but the moment when the Sun appears to stand still at its most southern point (so, furthest away from us in the northern hemisphere), before returning back towards the north. To put it another way, it's the moment in our annual journey around the Sun when the Earth's axis is tilted directly away from it (or directly towards it if you're reading this in Madagascar).

Notice that the first explanation I just gave - and the word solstice - is a geocentric view of things: we're talking about the Sun moving, rather than the Earth.  But that's what makes most intuitive sense (and of course it doesn't make any practical difference, since these motions are only relative).  Still, I was interested to see that that was the explanation the Met Office used in the "6 facts about the winter solstice" they published this morning.

One of their 6 facts was that the shortest day is "nine hours darker" than the longest day.  That made me wonder: Where?  Of course you know that the winter days are shorter in Aberdeen than they are in Aberystwyth - so at what latitude is it true that, as the Met Office say, the shortest day is 7 hours and 50 minutes long?

Peterhouse, Cambridge MS 75.I, "The Equatorie of the Planetis", f. 63v

That was a question that interested medieval astronomers too.  In the days before electricity, they were naturally more aware than us of the receding and returning daylight.  And there's lots of evidence of their scientific approach to the matter.  To take just one example, my favourite manuscript (from Peterhouse in Cambridge) features this table (right).

The title (in Latin) is "Table of the increase of the longest day over the equinoctial day, for all the habitable earth".  As you can see, there are two columns, which repeat 3½ times.  They are headed "altitude of the pole" and "half addition".

That's simpler than it may sound!  The altitude is that of the celestial pole - the height of the pole star above the horizon.  That height - an angle on the sphere of the sky - is equal to your latitude.  When the pole star is directly overhead, you're at the north pole.  So the "habitable earth" in this table is from 1° to 60° North (sorry, Icelanders).  The "half addition" tells you that what we are actually being given is the difference in the length of the afternoon (or morning) of the longest day - from noon to sunset, compared with the equinox.  It's given in degrees. To find the difference in hours, you divide by 15 (360° ÷ 24 hrs = 15).

The fact that we are given altitude rather than latitude, and additions in degrees rather than hours, reminds us that these medievals were astronomers and mathematicians.  They were interested in scientific questions, not just mundane practicalities.  And those questions involved some complex science.  To draw up a table like this, showing the different day lengths at different latitudes, you don't just need to know spherical trigonometry.  You also need to have an estimate for the axial tilt of the Earth.

And medieval astronomers did. (Though because they didn't think the Earth spun on an axis, it was called the obliquity of the ecliptic - the angle between the celestial equator and the Sun's annual path between the tropics of Cancer and Capricorn.)  Estimates varied - the obliquity itself has too, over time - between about 23½° and 24°.  So historians trying to find the sources of science through the ages can check these tables to see what parameters are being used, and work out where they came from.  The table above uses an obliquity of 23° 35', which was a value popularised by the 9th-century Arab astronomer Al-Battani, and used by a number of Europeans in the middle ages.

So can we use this table (produced by a 14th-century monk, John Westwyk) to work out where in the UK the Met Office's numbers are true?  You bet!  Their blog post gives 16 hours 38 minutes as the length of the longest day.  On the equinox, of course, it's exactly 12 hours.  So we're looking for a difference of 4 hours and 38 minutes.  Of course the table gives half-additions, in degrees; 4h38 ÷ 2, x 15 = 34.75, or 34° 45'.  The table above gives a value very close to that (34° 43') for a latitude of 52° 30' N - the latitude of Birmingham.  The Met Office headquarters is actually in Exeter (latitude 50° 43') - so maybe they didn't want to rub in the fact that they have a few minutes more light today than the rest of us...

May your days be merry and bright!

Medieval finger-counting on the BBC

"Hand of Bede" from Bodleian Library, Oxford,
MS Digby 56, f. 165v (12th century)

Yesterday I had an opportunity to present some medieval science on the BBC.  I had been asked to contribute to "Free Thinking" on Radio 3.  The theme of the programme was "Hands", so I decided to fill my allocated 4 minutes by talking about early medieval finger-counting.

You can listen to the full programme here - my short essay and interview start at 22 minutes. (You can also download Free Thinking as a podcast on iTunes.)

I also recorded this spur-of-the-moment clip, showing some numbers on my fingers.  A bit clumsy, but I only got one try at it!


If you want to read some more about finger-counting and hand-diagrams in the Middle Ages, I recommend this blog post by Irene O'Daly.  You can also read Bede's The Reckoning of Time in a great edition by Faith Wallis.

The start of summer?

Facebook greeted me today with this little graphic:

Given that this is the radar picture over the UK this morning, it's not surprising that several Facebook users felt a certain irony.

But in what sense is it the first day of summer? As the Met Office explain in a lovely clear blog post, it depends whether you're talking about the meteorological summer or the astronomical summer.  For our forecasting friends, summer began three weeks ago on 1 June.  (Though as my wife often reminds me, summer in Ireland is often thought of as beginning on 1 May.)

But of course I'm interested in the astronomical calendar.  There, summer begins at the summer solstice.  That's today.  In astronomical terms, the solstice occurs when the Earth's axis is most inclined towards the Sun.  Or to put it another way, it's when the Sun stops in its passage north, pausing directly over the Tropic of Cancer before beginning its return journey back towards the south.

Since our calendar years are of unequal length (remember 29 February?), the solstice doesn't occur at exactly the same time every year.  Normally it's on 21 June, but this year, because it's a leap year, it's on the 20th.  To be precise, the moment of solstice will be at 23:34 BST tonight.  After that the Sun will head back south and the days will get gradually shorter.

Medieval astronomers understood this very well.  In his Treatise on the Astrolabe, Chaucer explains that

the Head of Capricorn [start of the zodiac sign of Capricorn] is the lowest point that the Sun goes in winter, and the Head of Cancer is the highest point that the Sun goes in summer. And therefore understand well that any two degrees [of the ecliptic] that are alike far from either of these two Heads, are of alike declination, be it southward or northward; and the days of them are alike in length and the nights also, and the shadows alike, and the altitudes alike at midday forever. (II.16)

This makes the connection between the Tropic of Cancer and the zodiac sign of Cancer quite clear.  (Not the constellation Cancer though; the Sun won't get there for another month, because of the precession of the equinoxes.)  Chaucer points out that any two places that the Sun passes in the zodiac, which are equally far from one of the Heads/solstices, will have the same length days (and nights).

Making use of shadows - if there are any.

They'll also have the same declination - that is, the Sun will be equally far from the equator (which it crosses at the equinox).  The Sun's declination, combined with its noon altitude, allows Chaucer to find his latitude.  I'm sure you've noticed that the Sun gets higher in the sky in summer.  If you measure its altitude at noon, subtract the Sun's declination at that date, and then subtract the whole lot from 90°, you have your latitude.

Because the Sun is higher in the summer than in the winter, a shadow cast by any object at noon will be shorter.  Astronomers (and even architects) had, since the ancient Greeks if not the Babylonians, been well aware of the usefulness of shadows for marking the seasons; for finding local time, the direction of north, and the direction of sunrise and sunset.

Chaucer wasn't shy of dropping his astronomical knowledge into his poetry, of course.  In the Canterbury Tales, the Merchant describes the weather a few days before the solstice.  It's rather better than today's:

Bright was the day, and blue the firmament;
Phebus [the Sun] hath of gold his streams down sent
To gladden every flower with his warmnesse.
He was that time in Gemini, as I guess,
But little from his declination
Of Cancer, Jove's exaltation [an astrological reference to Jupiter].

Today the Sun will set further north than any other day this year.  But I can't guarantee the weather will be summery enough for you to see it.